 |
 |
 |
 |
 |
GURU
|
 |
This is an introduction to making simple patterns and molds. The methods used are little different than thousands of years ago. The minimum tools required are simple woodworking hand tools but machinery such as band saws and lathes are very helpful.
The mold we are making will be of plaster of Paris and can be used to cast aluminium, brass, bronze, silver, gold or zinc.
These methods can also be used to make a plaster "backup plate" for making sand molds. For cast iron or high melting point bronze sand molds are better than plaster.
|
 |

Figure 3 |
Patterns can be made of metal, wood, plastic or combinations of materials. Generally whatever is most convenient. For high production the durability must be considered.
This pattern is made of walnut and pine. It is a handle for a musical instrument. The walnut is the pattern, the pine if the sprue (where the metal is poured in).
|
 |
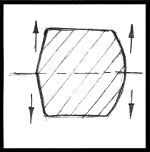
Figure 13 |
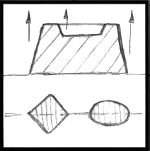
Figure 14 |
|
GURU
|
 |
The most important aspect to making a pattern is "draft". This is the angle on the side of the pattern that allows it to be smoothly removed from the mold. Very little slope is needed. 1/8" is about right on a 4" thick pattern.
The line on the pattern where the mold is split is called the "parting line". The pattern must have draft toward the parting line as shown in figures 13 and 14. Some parts have natural draft. The parting line can be on the center line of the part or on one side.
|
 |
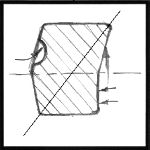
Figure 15 |
Undercuts or reverse slope will make it impossible to remove the pattern from the mold. The part to the left cannot be parted horizontally but it can be parted diagonally.
|
 |
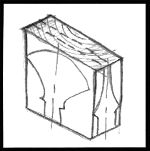
Figure 16 |
To make my handle pattern I started with a full scale drawing of the part in two views.
A copy of the drawing was glued to a squared block of wood.
The long end-view cuts were made on the band saw.
Then the stack of three pieces were taped together and the side view cut.
The result was a near net shape that required very little work.
|
 |

Figure 3 |
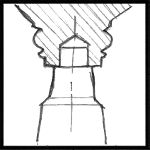
Figure 17 |
 |
GURU
|
 |
The round moulded part was turned on a small lathe and a hole bored concentric while the part was in the lathe.
The sprue was also turned on the lathe and had a stub to fit the pattern
|
GURU
|
 |
The pattern and sprue were finely finished and then lacquered.
Patterns don't have to be so pretty but they make nice sculptures when done.
|
 |

Figure 1 |

Figure 2 |
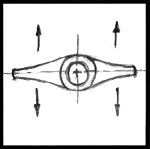
Figure 18 |
GURU
|
 |
This part was designed to be parted as shown. The "easy way" in this case is almost always the right way.
|
 |
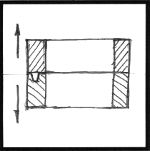
Figure 19 |

Figure 4 |

Figure 5 |
GURU
|
 |
To make a mold you will need a "mold box" or "flask".
It is a mold box when it is used to make a removable mold and a flask when the mold stays in the box while pouring the part.
|
GURU
|
 |
This mold box is made in two equal depth pieces and was sized for this particular part.
There are two dowels at the parting to align the two halves.
The dowels should be set asymetricaly so that the box only fits together one way.
The halves of this box are also hinges at one corner so that they can be opened for easy removal from the plaster mold.
|
 |

Figure 6 |
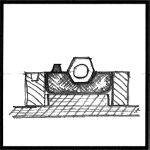
Figure 20 |
 |
GURU
|
 |
The pattern is set into the bottom half of the mold box on spacers.
The box is then filled with plasticine (modeling or oil) clay to the parting line on the part.
To reduce the amount of clay needed a filler board was set into the bottom of the box.
|
GURU
|
 |
Locator "buttons" were also set into the clay.
These are like steeply tapered dowels that align the two halves of the mold when it is removed from the mold box.
At least two are needed. Some are conical, some hemispherical.
I've shown one in the drawings. The "pattern" in the drawings is a simple symbolic shape.
|
 |
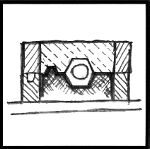
Figure 21 |
After the pattern is molded in to the clay the top half of the mold is installed and "parting compound" is painted onto the pattern, clay and wood.
I use a slurry of Ivory Soap applied with a soft watercolor brush. Other soaps do not work as well.
After the parting soap is dry, plaster of Paris is mixed and poured into the mold box.
As the plaster stiffens the top surface is "screed" off with a straight board so the surface is flat.
|
 |

Figure 8 |
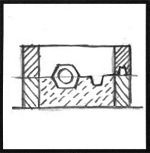
Figure 22 |
 |
GURU
|
 |
After the plaster sets the mold box is turned over and the clay removed.
If you are only making one mold you go ahead and apply parting soap and pour the second half of the mold.
In this case I wanted to make several molds.
Setting the part in the clay and setting up the locators and risers is most of the job.
So I will keep this first mold half as a "follower plate".
The pattern was removed and a after the plaster had dried a day it was coated with clear lacquer.
Lacquering is NOT done except on the reusable follower plate.
DO NOT lacquer mold parts.
After the lacquer dried, parting soap was applied and the pattern and riser pins replaced.
|
 |
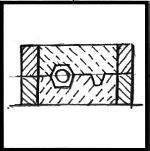
Figure 23 |
After reassembling the mold and pattern the second half of the mold was poured.
In this case I poured two top halves before removing the pattern and follower plate.
|
 |
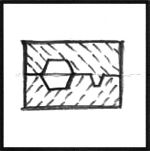
Figure 24 |

Figure 9 |

Figure 10 |
GURU
|
 |
After pouring two "tops" the bottoms of each mold was poured.
The pattern and riser pins are placed in the first part while the second is poured.
Parting soap is applied each time.
|
GURU
|
 |
Above you can see the two large locators for aligning the loose mold parts.
The riser pins were made from 1/4" dia. steel bar with a chamfer ground on the end that contacted the pattern.
The risers are so trapped air and gases can exit the mold cavity.
Sometimes you need them, sometimes not.
This is where the "art" of foundry work comes into play.
|
 |
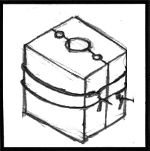
Figure 25 |
The finished mold halves are wired together and then "calcined".
Calcining is the heating of the mold to 1300 to 1400 deg. F. to cook off all the water in the mold including some that is bound chemically in the hardening process.
The metal should be poured while the mold is still hot from calcining to get the best results.
Otherwise if the mold is not used immediately it needs to be heated to at least 250 deg. F to drive off absorbed moisture just before pouring.
I did not properly calcine my molds and the results were rather interesting (below).
|
 |

Figure 1 |

Figure 11 |

Figure 12 |
GURU
|
 |
Here is the finished part and instrument.
This is a Kithara, an ancient Greek musical instrument from the classical period.
I've built several.
|
GURU
|
 |
The granular texture on the castings are the result of insufficient calcining.
I baked the molds at 350 deg F for four hours but this was far from hot enough.
On this job I made the pattern one day, did the casting the next, and had to have the instrument for show and tell the next!
On top of everything else I ran out of gas while melting the brass and had to resort to using an oxyacetylene rose bud to finish the pour.
Happily the "ancient" look of the castings suited the reproduction 2500 year old instrument.
The parts look sort of like they were retrieved from an old ship wreck on the bottom of the Mediterranean.
|
 |

Figure 8 |
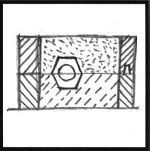
Figure 26 |
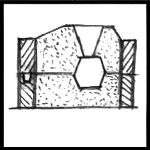
Figure 27 |
GURU
|
 |
The plaster follower plate can be used to make green sand or no-bake sand molds.
In this case the pattern is held by the plaster while the first half of the sand mold is rammed up.
Then the mold is turned over, the backing plate removed and the second half of the sand mold created.
The sand stays in the mold box so it is now a "flask".
A sprue must be cut or molded as shown above.
In this case the pattern would not have the pine "sprue on it.
Vents would be punched into the top half of the mold with a coat hanger sized wire.
Using the plaster follower plate makes producing molds for a center line parted part much easier.
|
GURU
|
 |
Questions? Comments?
|
Ntech
|
 |
How many casts can be expected from this type setup?
|
Mills
|
 |
Is calcining the first heating of the mold to rid it of moisture? Afterwards do you only need a good preheat?
|
Milt
|
 |
How large an item can you cast like you did?
|
GURU
|
 |
The mold is a one shot deal for all metals including low temperature alloys such as zinc.
|
Jim C.
|
 |
Good demo; different and interesting. I think I can cook off small molds in my gas forge.
|
Bryan
|
 |
Where does one get appropriate sand for making a sand mold?
|
GURU
|
 |
Calcining should be done immediately prior to the pour and the metal poured while the mold is still hot.
However, this is not always possible so if the calcined mold is stored say overnight it should be reheated to 350F to be sure it is dry.
|
Mills
|
 |
I guess if it is a one shot deal my question is moot, isn't it.? ;)
|
GURU
|
 |
How large is determined by how big a melt you have capacity for and how large a calcining oven.
|
GURU
|
 |
Yes, a gas forge with controls or all the doors open can be used for calcining. Controlled bonfires have also been used.
|
GURU
|
 |
Molding sand is available from foundry suppliers and jewelry suppliers.
IF you are going to do sand molding you should get one of C.W. Ammens books and study the subject.
There is a lot to it. You can use creek sand if you know how to pick and condition it.
|
Ntech
|
 |
If you need to make several items, what do you do differently so the mold can be reused?
|
Milt
|
 |
Thanks for the demo. I'd like to try using a mold sometime. I'll keep a copy of this demo.
|
Mills
|
 |
Nice demo, as usual, Jock. Is it necessary to always make a fresh mold or is there a material that allows multiple pours ?
|
GURU
|
 |
For multiple use you need a "permanent mold".
These are cast or machined from cast iron and steel.
Otherwise for metal casting the molds are destroyed with each cast.
However. . the same method above is used to make ceramic molds. You can make thousands of clay pieces from a plaster mold!
|
GURU
|
 |
Ceramic "hollow ware" is "slip cast" in plaster of Paris molds like the above. Clay "slip", a thin pourable water/clay mixture is poured into the plaster mold. After setting for a brief time (less than a minute) the excess slip is poured out of the mold. The clay next to the plaster has the water sucked out of it and stiffens rapidly. After a few more minutes the mold is opened and the "leather hard" clay part is removed from the mold. The sprue, risers and flash are trimmed off immediately. After the clay has air dried it is fired in a kiln to vitrify it.
|
GURU
|
 |
Plaster molds are made using the method above OR using "master" molds made from a hard high grade plaster. Plaster can be poured against plaster with simple soap parting and it does not stick to the other plaster part. Master molds are used to produce production molds. In this case each half of the master has the pattern cast into it. This speeds up the production of molds and prevents damage to the pattern.
|
GURU
|
 |
For permanent metal casting molds cast iron is best.
Making finished cast iron molds is expensive, equal to press die work requiring lots of machining.
Aluminium and zinc are commonly cast in permanent molds.
Copper alloys are generally cast by lost wax or the method above OR in sand molds.
|
|
 |
Links:
|




Demonstration by Jock Dempsey
May 30, 2001
The mold we are making will be of plaster of Paris and can be used to cast aluminium, brass, bronze, silver, gold or zinc.
These methods can also be used to make a plaster "backup plate" for making sand molds. For cast iron or high melting point bronze sand molds are better than plaster.
Figure 3
This pattern is made of walnut and pine. It is a handle for a musical instrument. The walnut is the pattern, the pine if the sprue (where the metal is poured in).
Figure 13
Figure 14
The line on the pattern where the mold is split is called the "parting line". The pattern must have draft toward the parting line as shown in figures 13 and 14. Some parts have natural draft. The parting line can be on the center line of the part or on one side.
Figure 15
Figure 16
The long end-view cuts were made on the band saw. Then the stack of three pieces were taped together and the side view cut. The result was a near net shape that required very little work.
Figure 3
Figure 17
Figure 1
Figure 2
Figure 18
Figure 19
Figure 4
Figure 5
The halves of this box are also hinges at one corner so that they can be opened for easy removal from the plaster mold.
Figure 6
Figure 20
Figure 21
After the parting soap is dry, plaster of Paris is mixed and poured into the mold box. As the plaster stiffens the top surface is "screed" off with a straight board so the surface is flat.
Figure 8
Figure 22
In this case I wanted to make several molds. Setting the part in the clay and setting up the locators and risers is most of the job. So I will keep this first mold half as a "follower plate". The pattern was removed and a after the plaster had dried a day it was coated with clear lacquer. Lacquering is NOT done except on the reusable follower plate. DO NOT lacquer mold parts. After the lacquer dried, parting soap was applied and the pattern and riser pins replaced.
Figure 23
Figure 24
Figure 9
Figure 10
Figure 25
The metal should be poured while the mold is still hot from calcining to get the best results. Otherwise if the mold is not used immediately it needs to be heated to at least 250 deg. F to drive off absorbed moisture just before pouring. I did not properly calcine my molds and the results were rather interesting (below).
Figure 1
Figure 11
Figure 12
Happily the "ancient" look of the castings suited the reproduction 2500 year old instrument. The parts look sort of like they were retrieved from an old ship wreck on the bottom of the Mediterranean.
Figure 8
Figure 26
Figure 27
Using the plaster follower plate makes producing molds for a center line parted part much easier.
iForge is an Andrew Hooper Production
HTML Copyright © 2001 Jock Dempsey, www.anvilfire.com