
Christoff Fredricks Cross
Demonstration by
Bill Epps
http://www.besmithy.com
14 June 2000

Christoff Fredricks Cross
Demonstration by
Bill Epps
http://www.besmithy.com
14 June 2000
Bill-Epps : |
Tonight's demo is the "Christoff Fredricks Cross" | |||||
Bill-Epps : |
I first saw this done by the Late/Great Francis Whittaker in the early '90s. | |||||
Bill-Epps : |
 |
 |
 |
|||
Bill-Epps : |
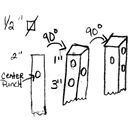
I made this one out of 1/2" square, but the one Francis demoed was out of 1", and I have seem them made out of as small as 1/4". Start by laying out the splits. On this size stock, I come back from the end 2" and make a center punch mark Rotate it 180 deg. and make another center punch mark 2" from end. | |||||
Bill-Epps : |
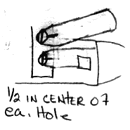
Then I go 90 deg. and go down 3" and make a center punch mark, and then come 1" from the end and make another center punch mark. I do this and rotate 180 deg. and do the same thing so you have the marks on both sides. | |||||
Bill-Epps : |
 |
 |
||||
Bill-Epps : |
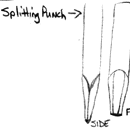
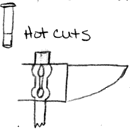
I make the bottom split first. I start w/a splitting punch first, then go to the hot cutter, but I make a split in each of the marks 1" from the end and 3" from the end. Go 1/2 way from each side. This means rotate and do it on each side. After I have gone all the way through w/the slitting punch, I use hot cutter and go 1/2 way through from the top; then flip it over and go 1/2 way through from other side. | |||||
Bill-Epps : |
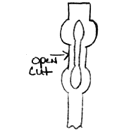 |
 |
||||
Bill-Epps : |
After you have made your splits 1/2 from each side, hopefully they will meet in the center. It is very important to keep the splits in the center of the bar. | |||||
Bill-Epps : |
 |
 |
||||
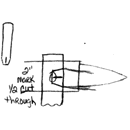
Bill-Epps : |
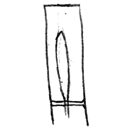
Now we go to the other side, rotate it 90 deg. and I use my splitting/slitting punch again on my mark and go completely through 1/2 from one side and 1/2 from the other side. Then use the hot cutter to split all the way out to the end. This should give you two splits 90 degs. apart that overlap from 3/4 to 1". | |||||
Bill-Epps : |
 |
 |
||||
Bill-Epps : |
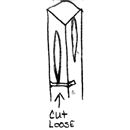
Now I use the hammer and square everything back up, close the slits back and get the bar back square. | |||||
Bill-Epps : |
 |
 |
||||
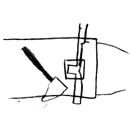
Bill-Epps : |
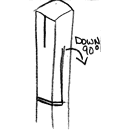
At the bottom of the bottom split, we cut 1/2 way from the top. This will be part that forms the top of the cross. Remember, this split will intersect with another split and you should be able to accomplish this by only cutting the bar 1/2 throug this time. | |||||
Bill-Epps : |
 |
 |
 |
|||
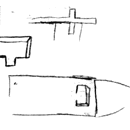
Bill-Epps : |
At the end of the bottom split, we bend it over the edge of the anvil and allow the top edge to come straight up. Then I go over the hardy hole and straighten the whole piece out with the two split legs down. Then I clamp it in the vice and hot rasp to clean up any rough edges. | |||||
Bill-Epps : |
 |
 |
 |
|||
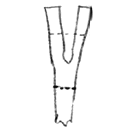
Bill-Epps : |
Then I use my cutting hardy again to spread the two bottom legs out and there is the cross w/an open diamond in the center. If the top leg of the cross is too long, just trim it off w/cutting hardy. Then I use a cross/pien or ball-pien either one to give little bit of flare and texture to the ends of the cross. | |||||
Bill-Epps : |
 |
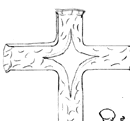 |
||||
Bill-Epps : |
Then I use the ball-pien to texture the whole thing to give it that "Old Rugged Cross" look. | |||||
Bill-Epps : |
|
|||||
Bill-Epps : |
For a base, you can either forge a tenon on the bottom and punch a base plate, I have seen people split the bottom and split 1/2 of it to give it 3 legs so it will stand up, but that is a matter of choice. I used a couple of these on a table that we just did for a minister. | |||||
Bill-Epps : |
Any questions? |
|||||
Jock-D : |
Bill, I'm a little unclear on the "opening up" step. | |||||
Steve-C : |
Bill I am not sure if I understand how the whole thing get opened up, but how thick is the cross when you get done | |||||
Bill-Epps : |
These are fun to do in front of a crowd and put on a good show. | |||||
Leah : |
how long was the stock you started with? | |||||
J-J : |
I think the double drwing for the opening up steps has a 90 degree to the left mistake in the cut.... | |||||
Rich-Hale : |
I think I will use JJ's idea and wokr this in modeling clay one time | |||||
Bill-Epps : |
Ok, Jock first: | |||||
Bill-Epps : |
 |
 |
 |
|||
Bill-Epps : |
 |
 |
||||
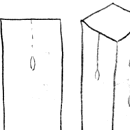
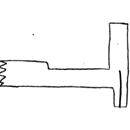
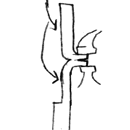
Bill-Epps : |
Ok the drawing on the left is shown wrong. The drawing on the right is correct. We have a split coming from the top, then we have a split 90 deg. at the bottom. At the bottom of the bottom split, the cut the bar 1/2 into. This allows it to unfold as you bend the end down over the anvil. | |||||
Bill-Epps : |
 |
 |
||||
Bill-Epps : |
Then I flatten the whole thing out w/ the "Top split down through the hardy hole". You end up w/1/2 X 1/4 thick and the part sticking down will still be 1/2" square. (if you are using 1/2" stock) That is what you clamp in the vice and use hammer to square it up. Then hot rasp. The drawing in the vice is showing the split incorrectly. It should be 90 deg. from what is showing. | |||||
Jock-D : |
I think I understand. Looks harder to draw than to do. . . | |||||
Bill-Epps : |
Yes, Jock, it is harder to draw than to do. These are the first drawings that Genia, the girl that works for me has done and I don't think she quite understood everything she was seeing. | |||||
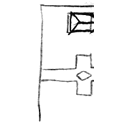
Steve-C : |
Bill can you show the other view that showes the top slit opened up? | |||||
Bill-Epps : |
 |
 |
 |
|||
J-J : |
So this step at the vice is pretty critical to the finished looks...maintaining the roll of the v. | |||||
bbb : |
yes jj, that is hard to maintain, but important | |||||
bbb : |
cheaters can use a hacksaw or bandsaw to split | |||||
Bill-Epps : |
We didn't get this real clear, but the two legs that are sticking down, I take to the hardy and drive the split down over the hardy to spread them out then flatten it all on the anvil. | |||||
J-J : |
Bill, the directions are really clear to someone who has done this before. It's just hard to visualize until you do one, i think. | |||||
Bill-Epps : |
Boys, now I got 3 swollen fingers, I got to soak this hand before it explodes, so are there any other questions??? | |||||
Paw-Paw : |
Bill, I got involved in answering an email and missed the end of the demo. One thing that i've see done to this cross you may have mentioned, but I didn't see it. If you upset all four ends of the cross and then flatten them out so that they "flare" out, the cross looks more "Celtic". | |||||
Steve-C : |
So when you get done how long are the horiztal arms? | |||||
bbb : |
if you draw out a part of the top, form a loop , you have a place for a necklace | |||||
Bryan : |
How long was the stock you started with? | |||||
J-J : |
Bryan, how tall you want your cross? :) | |||||
Bill-Epps : |
This piece was about 2' long, cause you need to be able to hold the piece as you work it rather than using tongs. You will cut off the excess after you get finished to put whatever kind of base you want to on it. We didn't show that, But it is a lot easier to use a longer piece just for handling it. | |||||
iForge is an Andrew Hooper Production
Copyright © 2000 Bill Epps
HTML Copyright ©2000 Jock Dempsey, www.anvilfire.com
Webmaster email: webmaster@anvilfire.com